Основным элементом многих оптических приборов и систем являются линзы (от лат. lens — «чечевица»). Линзой называют прозрачное тело, у которого хотя бы одна из поверхностей не является плоской.
Обычно линзы изготавливают из различных сортов оптического стекла, хотя в ряде случаев их делают из кварца, каменной соли, прозрачных пластмасс и других материалов. Чаще всего противоположные поверхности линзы имеют сферическую форму или же одна из поверхностей является сферической, а вторая — плоской. Поверхности линз могут иметь и другую форму, например цилиндрическую, параболическую и т. д. Однако мы ограничимся здесь рассмотрением только сферических линз.
Прямую, проходящую через центры обеих сферических поверхностей линзы, называют главной оптической осью. Если же одна из ограничивающих линзу поверхностей является плоской, то главная оптическая ось линзы проходит через центр сферической поверхности перпендикулярно её плоской поверхности.
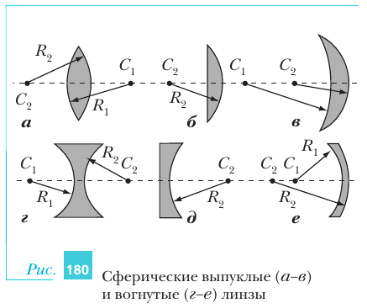
На рис. 180 показаны сечения сферических линз плоскостью, содержащей главную оптическую ось (пунктирные линии). Точками С1 и С2 обозначены центры сферических поверхностей линз, радиусы которых равны R1 и R2.
Если сферическая поверхность линзы и центр этой поверхности находятся по разные стороны от середины линзы, то радиус такой поверхности считают положительным, в противном случае — отрицательным. Например, оба радиуса линзы на рис.180,а положительны. У линзы, показанной на рис. 180,г, оба радиуса, напротив, отрицательны. Если толщина середины линзы больше толщины её края (рис. 180,а–в), то такую линзу называют выпуклой, если меньше (рис. 180, г–е) — вогнутой. У двух линз на рис.180 одна из поверхностей является плоской. Поэтому подобные линзы часто называют плосковыпуклыми (рис. 180,б) или плосковогнутыми (рис. 180,д). Направим на плосковыпуклую стеклянную линзу пучок лучей, параллельных её главной оптической оси (рис. 181). Из закона преломления следует, что такой пучок лучей после прохождения через линзу становится сходящимся. При этом чем дальше от главной оптической оси линзы проходит луч, тем на больший угол он отклоняется.
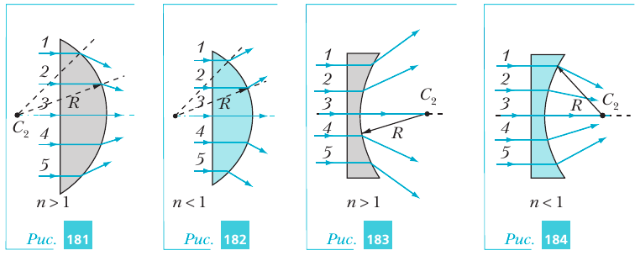
Линзы, которые преобразуют падающий на них параллельный пучок света в сходящийся, называют собирающими.
Используя закон преломления, можно доказать, что параллельный пучок лучей, падающий на плосковыпуклую линзу, показатель преломления материала которой меньше показателя преломления окружающей среды, выходит из линзы расходящимся (рис. 182).
Линзы, которые преобразуют падающий на них параллельный пучок света в расходящийся, называют рассеивающими.
Теперь сравним ход лучей, угол падения которых на передние плоские поверхности двух плосковогнутых линз равен нулю (рис. 183 и 184). Первая линза изготовлена из материала, показатель преломления которого больше показателя преломления окружающей среды. Из закона преломления следует, что выходящий из неё пучок лучей будет расходящимся. Следовательно, такая линза является рассеивающей. Вторая линза изготовлена из материала, показатель преломления которого меньше показателя преломления окружающей среды. Выходящий из неё пучок света является сходящимся. Следовательно, такая линза является собирающей.
Линзу называют тонкой, если модули радиусов R1 и R2 ограничивающих её поверхностей много больше толщины линзы.
Если линза является тонкой, то расстоянием между двумя точками пересечения главной оптической оси с ограничивающими линзу поверхностями можно пренебречь. Поэтому можно считать, что эти две точки совпадают. Эту точку называют оптическим центром линзы. При этом считают, что ограничивающие линзу поверхности лежат в одной плоскости, перпендикулярной главной оптической оси линзы и проходящей через её оптический центр. Эту плоскость называют главной плоскостью линзы. Главную плоскость собирающей линзы на чертежах изображают так, как показано на рис. 185,а. Изображение рассеивающей линзы показано на рис. 185,б. На этих рисунках точка О — оптический центр, а штрих-пунктирная линия — главная оптическая ось линзы. Прямую, проходящую через оптический центр линзы и не совпадающую с главной оптической осью, называют побочной оптической осью.
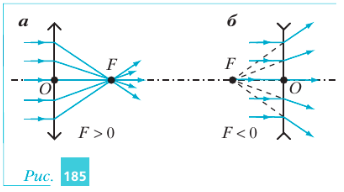
Действительно, для таких лучей центральную часть тонкой линзы (часть линзы вблизи её оптического центра) можно считать тонкой плоскопараллельной пластинкой. Вы уже знаете, что любой луч, проходящий через такую пластинку, не изменяет направления своего распространения. Параллельным же смещением луча можно пренебречь, поскольку толщина пластинки в данном случае пренебрежимо мала. Опыты и расчёты показывают, что все лучи, падающие на тонкую собирающую линзу параллельно её главной оптической оси, после преломления в линзе пересекаются в одной точке F, лежащей на этой оси (см. рис. 185,а). Эту точку называют главным фокусом собирающей линзы.
Расстояние от главного фокуса собирающей линзы до её оптического центра называют фокусным расстоянием этой линзы. Это расстояние, так же как и сам фокус, обозначают буквой F. Фокусное расстояние собирающей линзы положительно. Если параллельный пучок лучей падает на рассеивающую линзу, то в одной точке будут пересекаться продолжения выходящих из линзы лучей (на рис. 185,б эти продолжения показаны пунктирными линиями). Эту точку называют главным фокусом рассеивающей линзы. Фокусным расстоянием рассеивающей линзы называют расстояние от её главного фокуса до оптического центра, взятое со знаком «−». Фокусное расстояние рассеивающей линзы отрицательно.





Поделиться с друзьями: