Небесные координаты

     Чтобы лучше понять небесные координаты, сначала вспомним как мы определяем координаты своего положения на земле: 

  

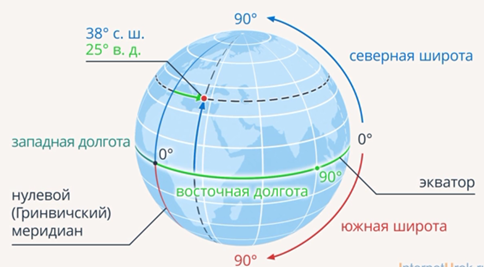
Теперь выделим важнейшие  круги на небесной сфере:

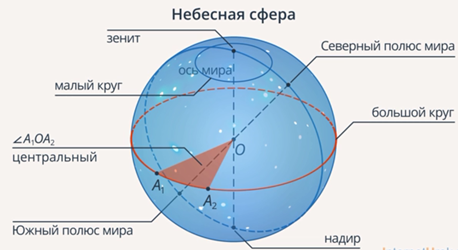
• математический горизонт – большой круг, плоскость которого перпендикулярна отвесной линии;
• небесный экватор – большой круг, плоскость которого перпендикулярна оси мира;
• небесный меридиан – большой круг, проходящий через зенит и Северный полюс мира (или через надир и Южный полюс мира) 

     Наблюдатель (человек) находится на Земле, а значит, испытывает действие силы тяжести F=mg. Данная сила направлена к центру Земли, то есть перпендикулярно по отношению к поверхности планеты в месте наблюдения. Таким образом, вектор силы тяжести направлен вдоль вертикальной линии, называемой линией отвеса (отвес - инструмент, состоящий из тонкой нити и грузика на её конце, позволяющий судить о правильном вертикальном положении). Линия отвеса пересекает небесную сферу в двух точках. Та из них, которая находится над головой наблюдателя, называется зенитом, противоположная ей – надиром. Плоскость, перпендикулярная вертикали (линии отвеса) и проходящая через центр сферы (глаз человека), пересечет небесную сферу по линии истинного математического горизонта. Математический горизонт не совпадает с видимым горизонтом, который может быть испещрен силуэтами, например, зданий или деревьев. Вот и получилось построение, изображенное условно на рис. 1. В дальнейшем в такого рода чертежах мы не будем изображать Землю и наблюдателя, не забывая, однако, о том, что в центре небесной сферы всегда мысленно помещают глаз наблюдателя. Как бы далеко в космосе ненаходились звезды, они все будут  казаться наблюдателю (глазу человека) близко расположенными и проецироваться  под разными углами на круге склонения небесной сферы.

 

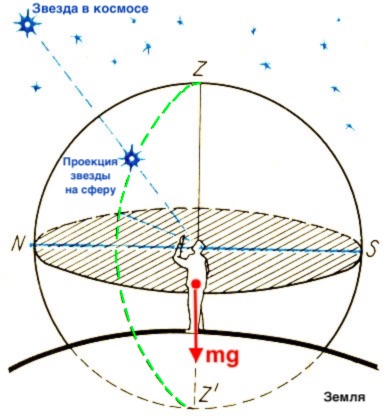
Рис. 1. Небесная сфера, наблюдатель и Земля

Движение Солнца по небесной сфере проходит через важные точки, которые необходимо запомнить:

                               точка весеннего равнодействия - в созвездии Овна

                               точка осеннего равнодействия   - в созвездии Весы

                               точка летнего солнцестояния     - в созвездии Рак

                               точка зимнего солнцестояния    - в созвездии Козерог

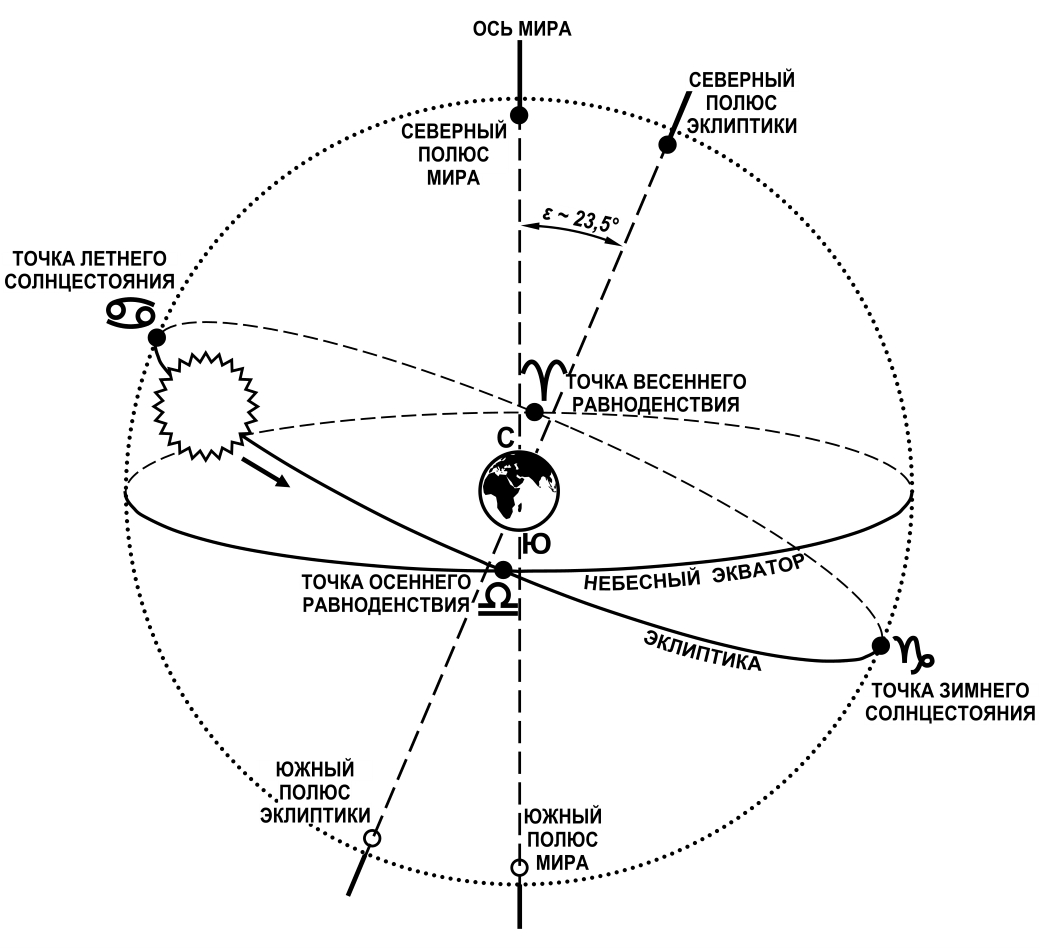
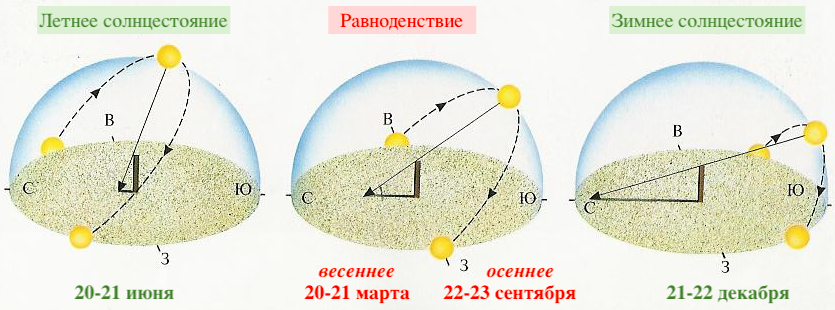
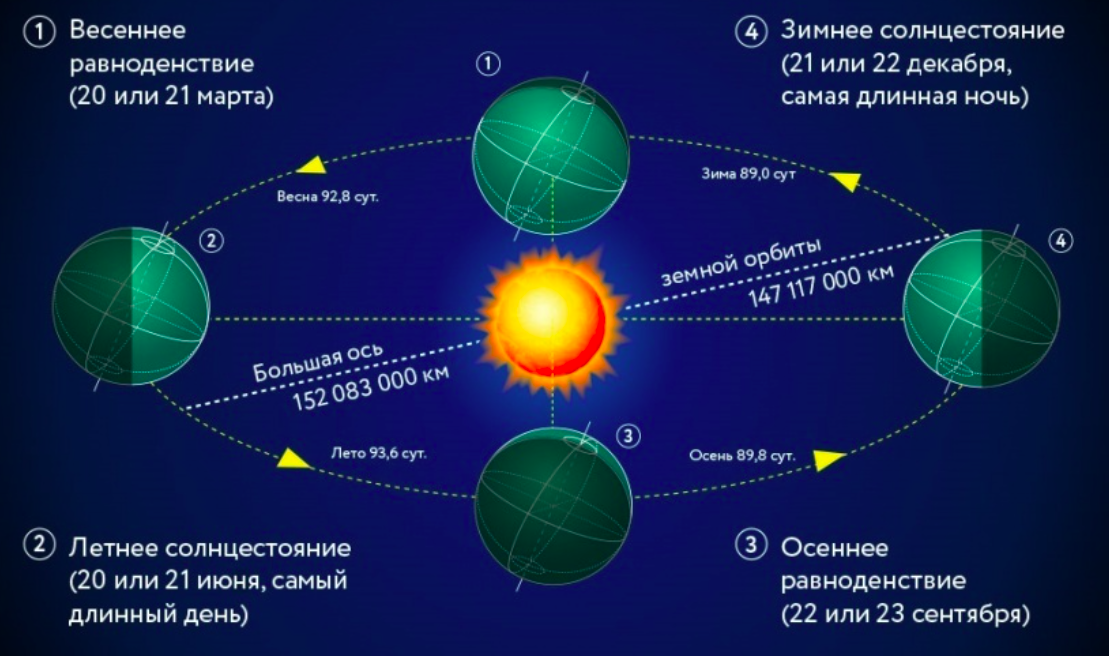
Равноденствие — это астрономическое явление, когда центр Солнца в своём видимом движении по эклиптике пересекает небесный экватор.

Солнцестояние — это астрономическое событие, при котором Солнце над горизонтом в истинный полдень находится на максимальной (летнее солнцестояние) или минимальной высоте (зимнее солнцестояние). В эти дни высота почти не изменяется — Солнце словно «стоит на месте». В ходе солнцестояний Солнце достигает максимальной высоты склонения к северу или югу относительно экватора Земли.

 Древние, конечно, давно заметили, что звездное небо как единое целое вращается вокруг наблюдателя. Не зная истинной причины этого явления (вращение Земли), они принимали его таким, каким видели. Все их наблюдения в конечном итоге позволили получить разные системы координат небесной сферы, в рамках которых одни и те же точки использовались и назывались по разному. Точки, в которых небесный экватор пересекает истинный горизонт (рис.1), называются точками востока Е (East) и запада W (West). Две другие точки горизонта, равноудаленные от них, называются точками севера N (Nord) и юга S (Sud), а прямая, их соединяющая,— полуденной линией (рис. 2). Только не путайте эти названия с северным и южным полюсами мира небесной сферы. Окружность, проходящая через полюса мира, зенит и надир, называется небесным меридианом.

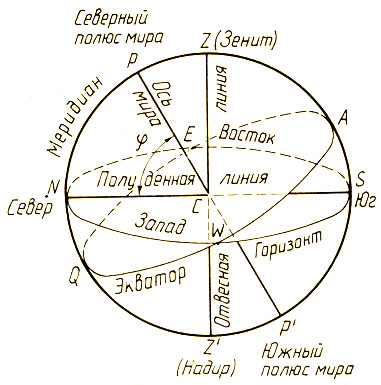
Рис. 2. Основные точки и линии небесной сферы

    В китайских хрониках сообщается, что около 1100 г. до н. э. китайский астроном Чу Конг измерил наклон эклиптики к экватору и нашел его равным 23°54'. Как он это сделал? Двигаясь по эклиптике, Солнце все время меняет угловое расстояние от экватора. 22 июня, вдень летнего солнцестояния, Солнце находится в самой "верхней" точке эклиптики (точке летнего солнцестояния), т.е. в наибольшем удалении от экватора к северному полюсу мира. Пусть в этот день в полдень, когда Солнце находится над точкой юга, его угловая высота над горизонтом равна h_max. Через полгода, когда Солнце будет в точке зимнего солнцестояния, его полуденная высота пусть равна h_min. Нетрудно сообразить, что угол ε наклона эклиптики к экватору определится формулой

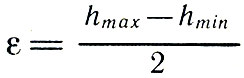
Что же касается полуденной высоты Солнца, то она определяется без всякого труда с помощью угломерных инструментов, которые изложены на данном сайте в разделе "Что и как изучает астрономия?" Величина ε имеет большое значение в астрономии. Она множество раз уточнялась разными астрономами и в настоящее время принимается равной 23°26'. Заметим, что на протяжении веков по ряду причин она слегка изменяется.

   Ориентация во времени и пространстве есть главная задача практической астрономии. Вопрос "когда?" решается указанием момента времени. Другой вопрос - "где?" требует введения координат, т. е. системы отсчета, в которой фиксируется положение небесного объекта. Так как на небесной сфере возможны лишь угловые измерения, небесные координаты представляют собой системы углов, определяющих место светила на небосводе.

 

1. Горизонтальная система координат

 

Под угловой высотой или просто высотой светила h понимают угол между лучом, идущим из центра небесной сферы на светило, и плоскостью горизонта. Дополнительный угол z называется зенитным расстоянием светила.

 

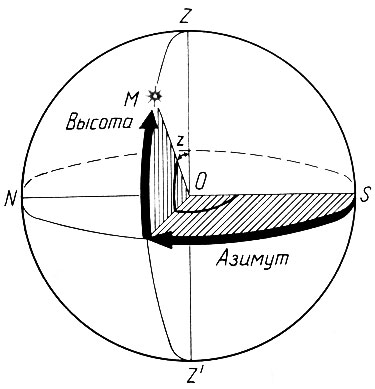
Рис. 3. Горизонтальные координаты

Проведем через зенит и светило полуокружность, именуемую вертикалом. Угол, который образует плоскость вертикала с плоскостью небесного меридиана, называется азимутом. Этот угол отсчитывается от точки юга к западу (от 0 до 360°)^*.

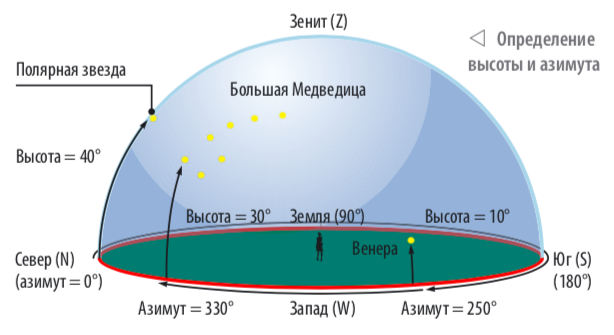
Значения азимута и высоты полностью определяют положение точки на небесной сфере. (В геодезии азимуты отсчитываются от точки севера к востоку). У небесных светил, кроме тех, которые находятся в полюсах мира, эти координаты все время меняются, что делает горизонтальную систему очень неудобной.

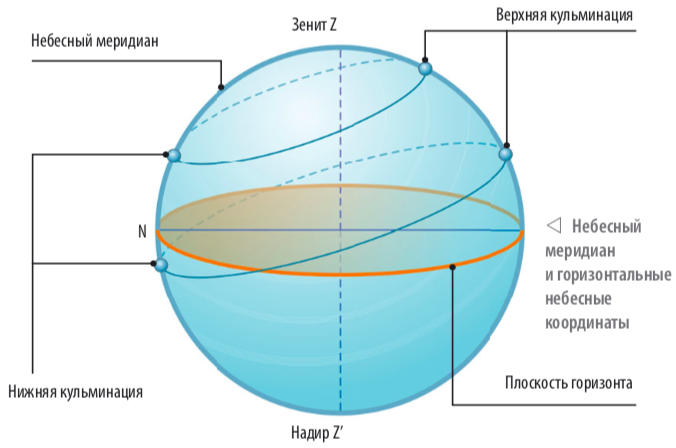
Кульминация — это прохождение центра светила через небесный меридиан в процессе его суточного движения. Другими словами — это прохождение центром светила точки пересечения суточной параллели светила и небесного меридиана.

 

 

 2. Экваториальная система координат

 

    Экваториальные координаты очень удобны тем, что не зависят от вращения небесной сферы, поэтому сейчас получили наибольшее применение. Они очень похожи на географические координаты — широту и долготу. Роль широты играет склонение δ, а роль долготы — прямое восхождение (рис. 4). 

Прямое восхождение — это длина дуги небесного экватора от точки весеннего равноденствия до круга склонения.

Склонение светила — это угловое расстояние светила от плоскости небесного экватора, измеренного вдоль круга склонения. 

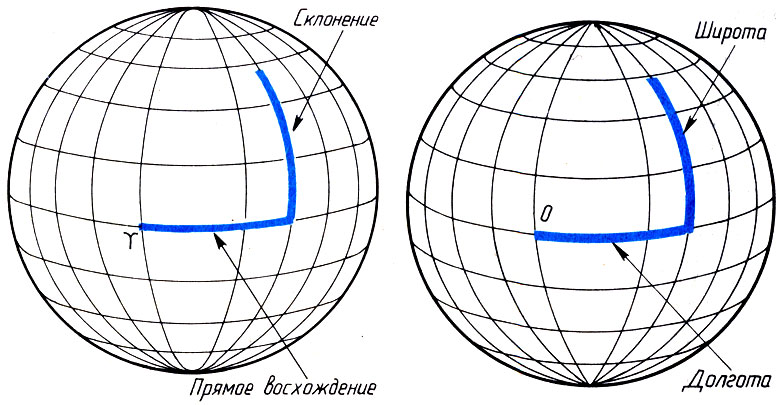
Рис. 4. Экваториальные (слева) и географические (справа) координаты

Склонение δ измеряется в градусах, причем считается положительным к северу от небесного экватора и отрицательным к югу от него. Прямое восхождение принято измерять в часах, минутах и секундах. При этом 360° соответствует 24 ч, откуда каждый час прямого восхождения соответствует 15°.

Построение небесной сферы будет неполным, если не уточнить, от чего зависит угол наклона оси мира к плоскости горизонта.

Около 320 г. до н. э. греческий астроном, географ и мореплаватель Питеас, убежденный в шарообразности Земли, впервые доказал, что угловая высота полюса мира над горизонтом всегда равна географической широте места.

Рассмотрите внимательно рис. 5. Так как видимое суточное вращение небосвода вызвано действительным вращением Земли вокруг оси, то ось мира, проведенная в данном пункте наблюдения, параллельна земной оси. Но тогда географическая широта места φ и угловая высота полюса мира над горизонтом h_p есть углы со взаимно перпендикулярными сторонами, равенство которых доказывается в элементарной геометрии.

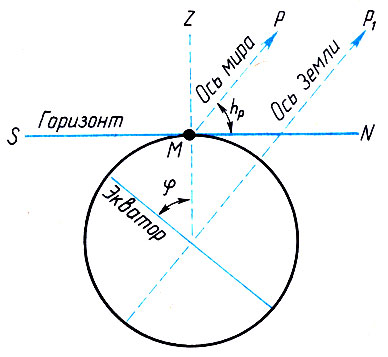
Рис. 5. Теорема о высоте полюса мира

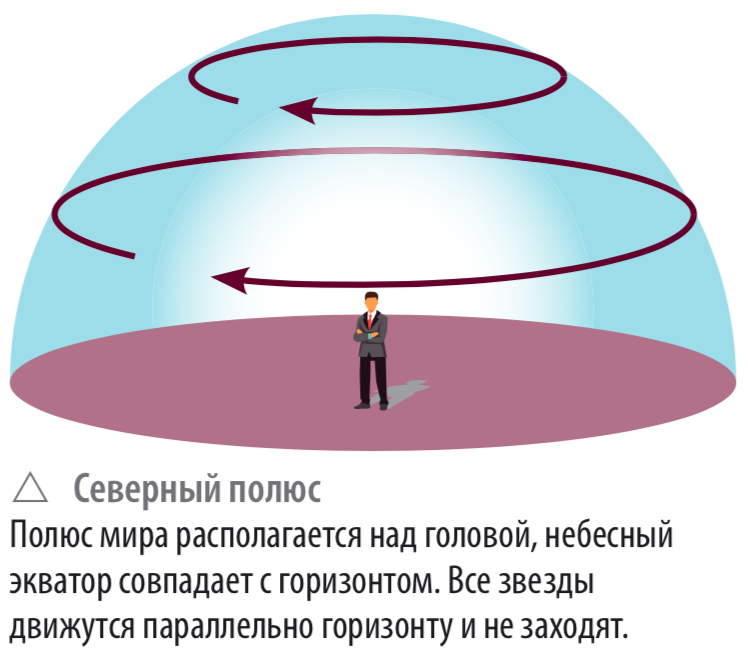
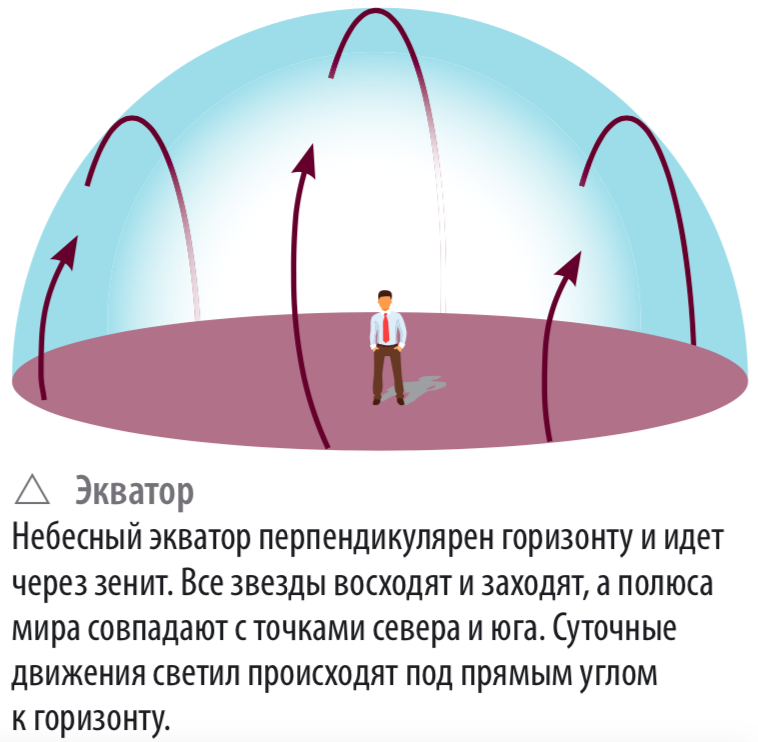
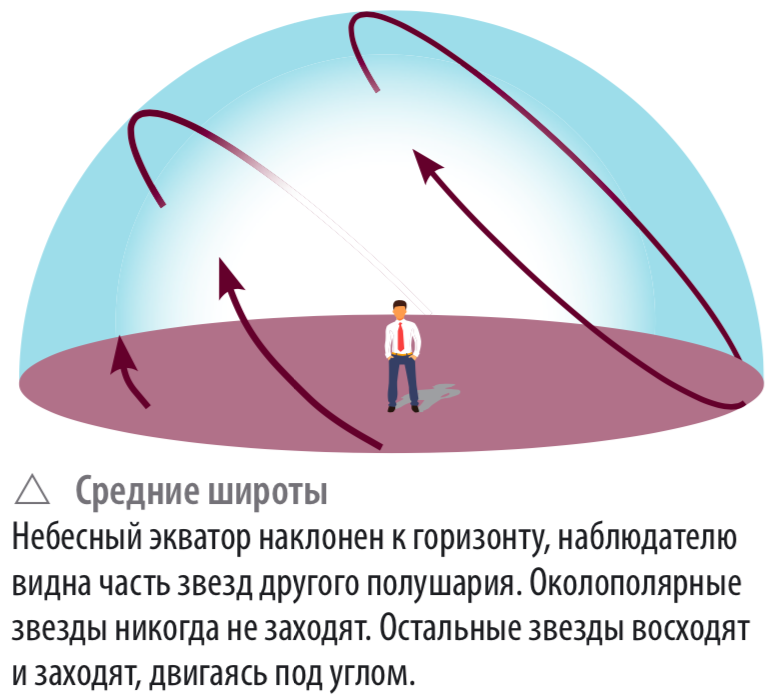
Для Москвы φ = 56°, и на московском небе есть никогда не заходящие и никогда не восходящие звезды. На полюсах Земли (φ = ±90°) над горизонтом видно всегда какое-нибудь одно полушарие звездного неба, причем звезды движутся параллельно горизонту. На земном экваторе (φ = 0°) другая картина: ось мира лежит в плоскости горизонта, все звезды восходят и заходят, причем их видимые пути перпендикулярны горизонту.

 

Небесная сфера - очень удобное геометрическое построение. Возникшее еще в те времена, когда люди верили в реальность вещественных, "хрустальных" небесных сфер, оно сохранилось и в наши дни как какая-то математическая абстракция, совершенно необходимая для описания видимых движений небесных тел.